# Iniciamos importando as bibliotecas e modulos necessários
import numpy as np
import numpy.random as npr
import matplotlib.pyplot as plt
# configuração output dos plots
plt.rcParams['figure.figsize'] = [12, 8]
plt.rcParams['figure.dpi'] = 100
# setando uma seed para reprodutibilidade
npr.seed(123)
# Inicializando a variável passeio aleatório
passeio_aleatorio = [0]
# aqui defino range(observações) em que observações é a numero total de observações
for x in range(100) :
passo = passeio_aleatorio[-1]
dado = npr.randint(1,7)
if dado <= 2:
passo = max(0, passo - 1)
elif dado <= 5:
passo = passo + 1
else:
passo = passo + npr.randint(1,7)
passeio_aleatorio.append(passo)
# Plot passeio_aleatorio
plt.plot(passeio_aleatorio)
# Strings
xlab = 'Observações'
ylab = 'Passos'
title = 'Passeio Aleatório'
# Add axis labels
plt.title(title)
plt.xlabel(xlab)
plt.ylabel(ylab)
plt.show()
# Show the plot Passeio Aleatório
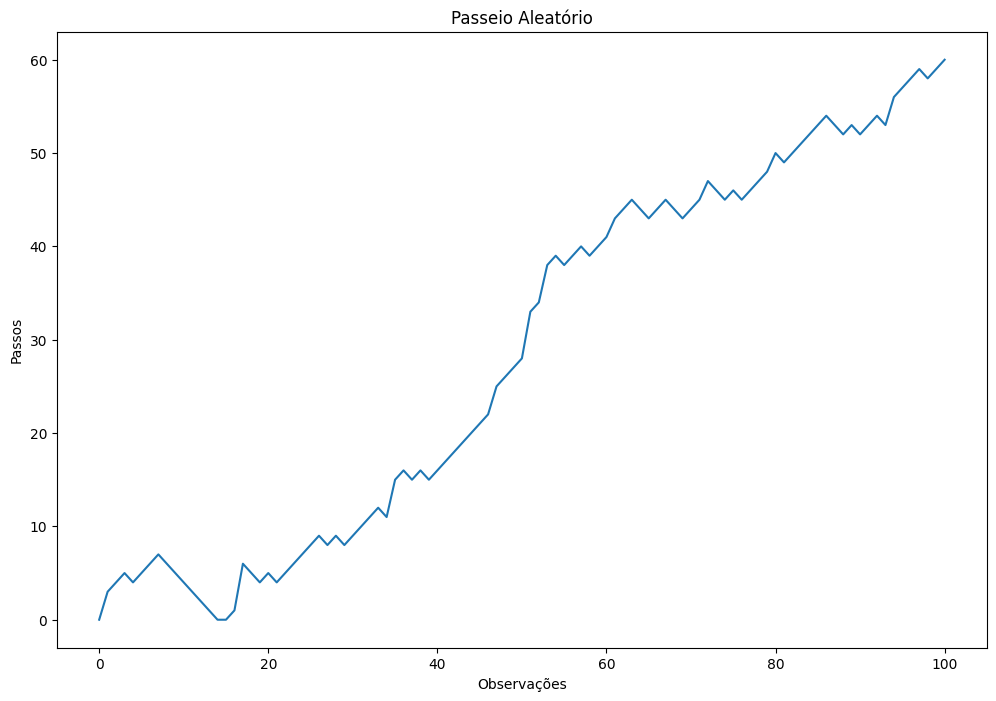
Passeio Aleatório (random walk)
O passeio aleátorio (random walk) é um dos processos estocásticos mais comuns, trata-se de uma cadeia de Markov em tempo discreto. Vamos simular este processo usando python. Para manter as coisas simples, vamos impor as seguintes regras:
Começamos no tempo 0 e iremos até o tempo 100, vamos usar um dado para ditar quando passos iremos dar em tempo t. A partir disso temos: * Se o resultado do dado for 1 ou 2 iremos voltar um passo atras, ou permanecer no 0. * Se o resultado do dado for 3, 4, ou 5 damos um passo a frente. * Se o resultado do dado for 6, jogamos o dado novamente e somamos 6 ao resultado do segundo lançamento, por exemplo: 6 + 2=8, neste caso andaremos 8 passos.
No código abaixo, vamos construir a base para nossa simulação.
# inicializando e preenchendo passeios
passeios = []
for i in range(10) :
passeio_aleatorio = [0]
for x in range(100) :
passo = passeio_aleatorio[-1]
dado = np.random.randint(1,7)
if dado <= 2:
passo = max(0, passo - 1)
elif dado <= 5:
passo = passo + 1
else:
passo = passo + np.random.randint(1,7)
passeio_aleatorio.append(passo)
passeios.append(passeio_aleatorio)
# convertendo passeios para um numpy array: np_ps
np_ps = np.array(passeios)
# transpondo np_ps
np_ps_t = np.transpose(np_ps)
# Plotando np_ps_t, cada
xlab = 'Observações'
ylab = 'Passos'
title = 'Passeios Aleatórios'
lg=[]
for x in range(10):
lg.append("passeio " + str(x + 1))
fig, ax = plt.subplots()
plt.title(title)
plt.xlabel(xlab)
plt.ylabel(ylab)
ax.plot(np_ps_t)
ax.legend(lg)
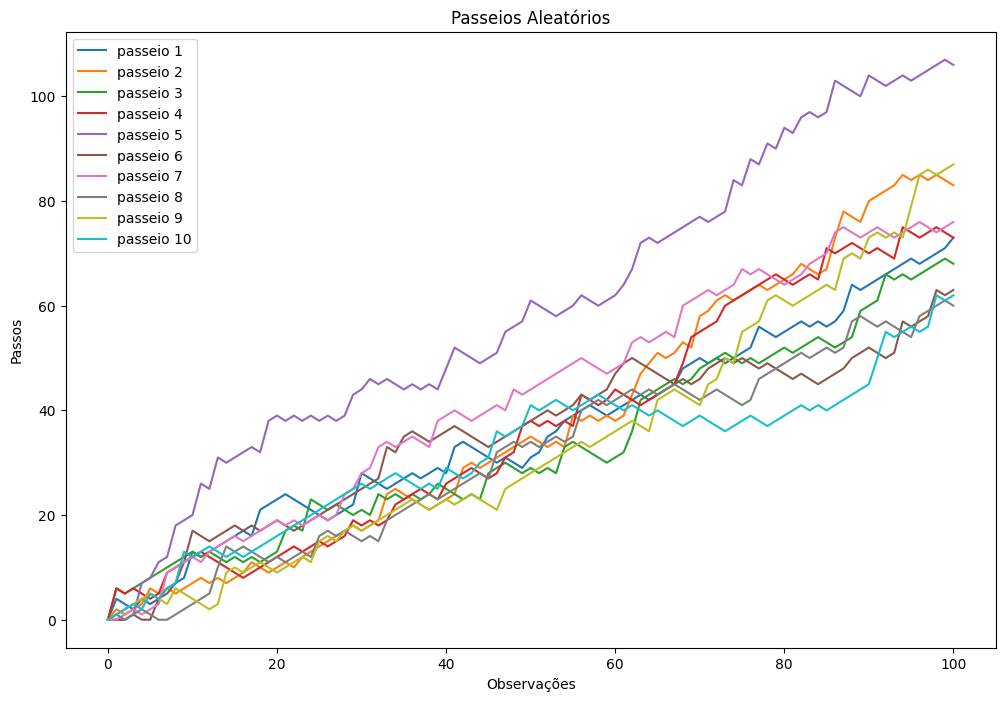
plt.show()Podemos agora, extrapolar o numero de simulações afim de encontrar a distribuição de probabilidade para este caso. Aqui simulamos 10000 vezes os passeios.
# inicializando e preenchendo passeios
passeios = []
for i in range(10000) :
passeio_aleatorio = [0]
for x in range(100) :
passo = passeio_aleatorio[-1]
dado = np.random.randint(1,7)
if dado <= 2:
passo = max(0, passo - 1)
elif dado <= 5:
passo = passo + 1
else:
passo = passo + np.random.randint(1,7)
passeio_aleatorio.append(passo)
passeios.append(passeio_aleatorio)
# convertendo passeios para um numpy array: np_ps
np_ps = np.array(passeios)
# transpondo np_ps
np_ps_t = np.transpose(np_ps)
ends = np_ps_t[-1]
# Plot histogram of ends, display plot
plt.hist(ends, edgecolor='white', linewidth=0.5)
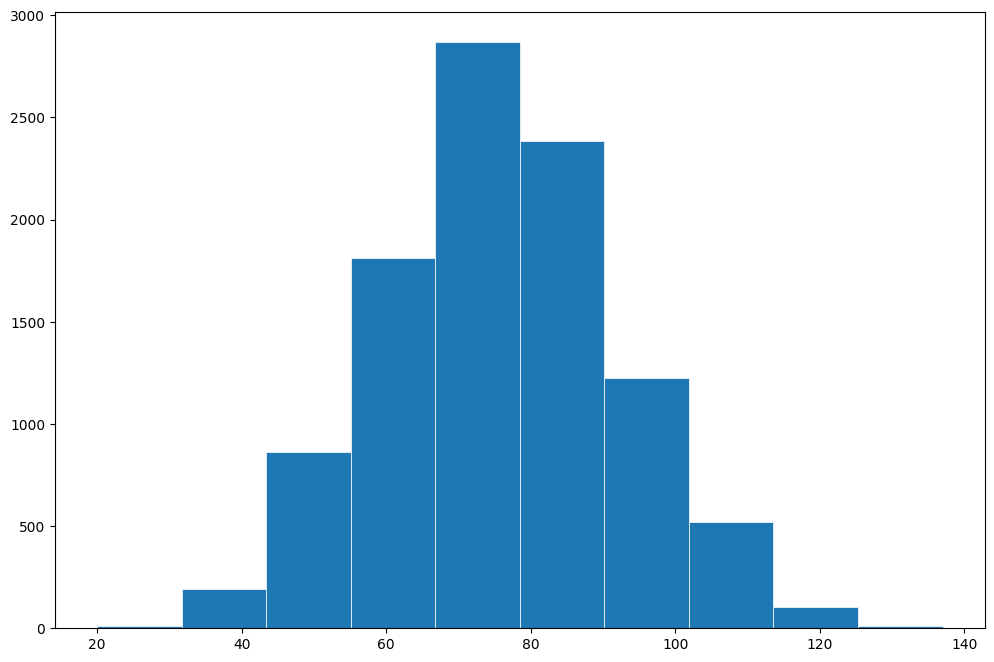
plt.show()O histograma acima mostra em aproximadamente 3000 das 10000 simulações realizadas, o ultimo passo dado no tempo t=100 será em aproximadamente o 75. Com base nos resultados encontrados, é possível encontrar a probabilidade de o ultimo passo ser maior que um valor x, por exemplo: \(P(\text{ passo }>x)= (\text{ número de passos > x })/ (\text{ número de simulações } )\)
#Probabilidade de que o ultimo passo seja maior que 60 é:
len(ends[ends>=60])/100000.8389